Problems tagged with "symmetric matrices"
Problem #43
Tags: linear algebra, quiz-03, symmetric matrices, eigenvectors, lecture-04, linear transformations
The figure below shows a linear transformation \(\vec{f}\) applied to points on the unit circle. Each arrow shows the direction and relative magnitude of \(\vec{f}(\vec{x})\) for a point \(\vec{x}\) on the circle.
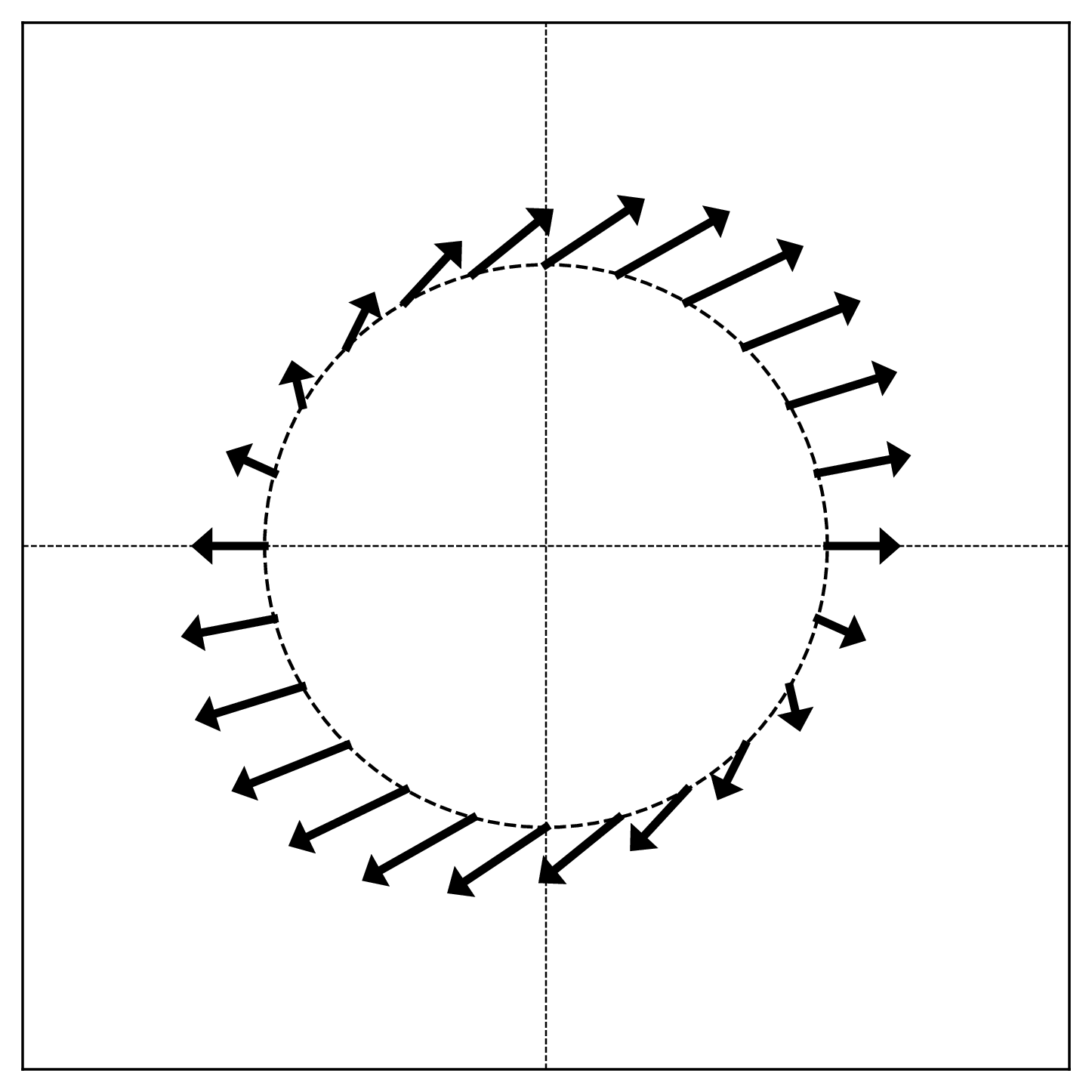
True or False: The linear transformation \(\vec{f}\) is symmetric.
Solution
False.
Recall from lecture that symmetric linear transformations have orthogonal axes of symmetry. In the visualization, this would appear as two perpendicular directions where the arrows point directly outward (or inward) from the circle.
In this figure, there are no such orthogonal axes of symmetry. The pattern of arrows does not exhibit the characteristic symmetry of a symmetric transformation.